比例线段
对于四条线段 a,b,c,d 如果两条线段的比(即它们长度的比)与另两条线段的比相等,如 ba=dc(ad=bc),我们就说这四条线段成比例。
比例性质
ba=dc⇔ca=db
ba=cb→b2=ac
比例中项
如果 a、b、c 三个量成比例即 a:b=b:c,b 叫做 a 和 c 的比例中项。
例子
1:2=2:4
2 是 1 和 4 的比例中项。
平行线分线段成比例
性质
两条直线被一组平行线所截,所得的对应线段成比例。
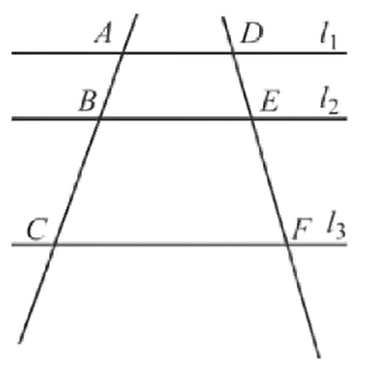
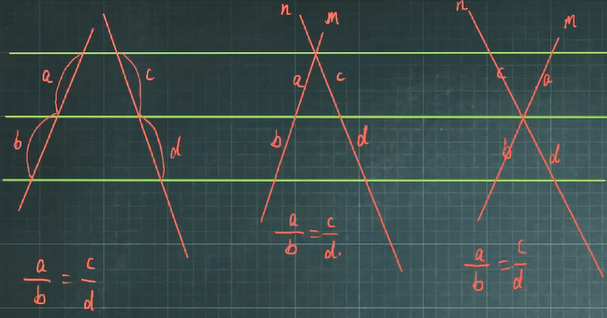
几何语言
∵l1//l2//l3
∴BCAB=EFDE(上比下 = 上比下)
∴ACAB=DFDE(上比全 = 上比全)
∴ACBC=DFEF(下比全 = 下比全)
相似三角形
定义
在 △ABC 和 △A′B′C′ 中,
如果 ∠A=∠A′,∠B=∠B′,∠C=∠C′,A′B′AB=B′C′BC=A′C′AC=k,
即三个角分别相等,三条边成比例,
我们就说 △ABC 与 △A′B′C′ 相似,相似比为 k。
相似用相似符号“∽”表示,读作“相似于”。
△ABC 与 △A′B′C′ 相似,记作 △ABC∽△A′B′C′。
判定
预备定理
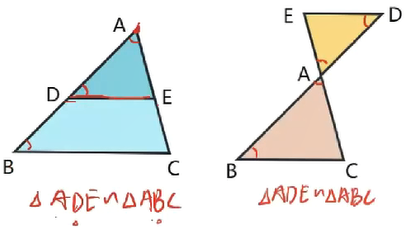
平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似。
几何语言
∵DE//BC
∴△ADE∽△ABC
判定定理 AA
两角分别相等的两个三角形相似。
几何语言
∵∠A=∠A′,∠B=∠B′
∴△ABC∽△A′B′C′
判定定理 SAS
两边成比例且夹角相等的两个三角形相似。
几何语言
∵A′B′AB=A′C′AC,∠A=∠A′
∴△ABC∽△A′B′C′
判定定理 SSS
三边成比例的两个三角形相似。
几何语言
∵A′B′AB=B′C′BC=A′C′AC
∴△ABC∽△A′B′C′
性质
性质 1
相似三角形的对应角相等。
几何语言
∵△ABC∽△A′B′C′
∴∠A=∠A′,∠B=∠B′,∠C=∠C′
性质 2
相似三角形的对应边成比例。
几何语言
∵△ABC∽△A′B′C′
∴A′B′AB=B′C′BC=A′C′AC=k
性质 3
相似三角形对应高的比,对应中线的比与对应角平分线的比都等于相似比(对应线段的比值均为相似比)。
性质 4
相似三角形周长的比等于相似比。
几何语言
∵△ABC∽△A′B′C′
∴C△A′B′C′C△ABC=k
性质 5
相似三角形面积的比等于相似比的平方。
几何语言
∵△ABC∽△A′B′C′
∴S△A′B′C′S△ABC=k2
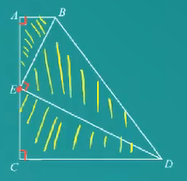
一线三垂直相似模型
如果:∠A=∠C=∠BED=90°,又 E 为 AC 中点,则:△ABE∽△CED∽△EBD。
鸡在河上(积在和上)
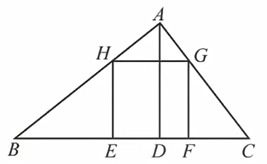
在 △ABC 中,边 BC=x,高 AD=y,四边形 EFGH 是边长为 a 的正方形,则有:
a=x+yxy
手拉手模型
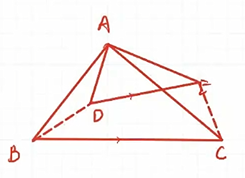
△ABC∽△ADE⟺△ABD∽△ACE
∠BAC=∠DAE⟺∠BAD=∠CAE
ADAB=AEAC⟺ACAB=AEAD





